A chatbot that helps students pick a university abroad for their next mobility program.
Two of the members in our group had just been through the stressful process of choosing a university abroad for our Erasmus+ mobility next year. The large amount of possibile destinations and the particularities of each case (compatibility of academic calendars, university reputation, affordable accommodation, possibility of developing the final thesis, etc.) are a common cause for many sleepless nights.
So for our project at HackUPC 2021 we decided to make a tool that helps undecided students sort the long list of universities and choose the one that best suits their interests.
Mobility destination picker is a Telegram Bot with a similar behaviour to the popular game Akinator. Through a series of simple questions and 5 possible answers, the program finds the universities that best fit the user while trying to keep the number of questions as small as possible.
How it works
Student’s perspective
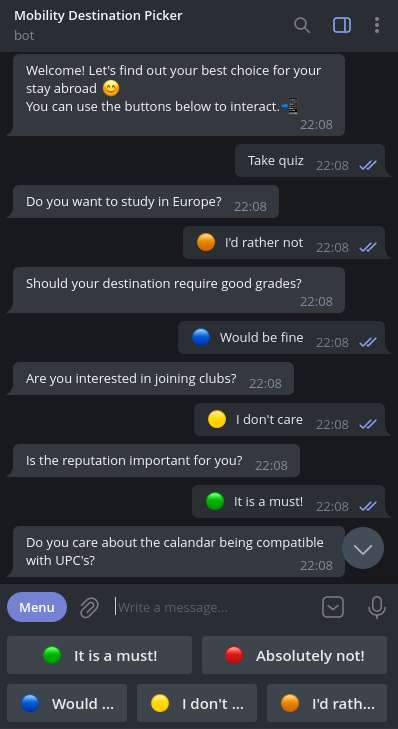
The student talks with the bot on Telegram, either from the phone, desktop or web application. The interaction is very user friendly: start the conversation with /start and follow the instructions on-screen. There are help and instruction commands as well.
The bot will then ask a series of questions to find out about the user interests. If will avoid irrelevant questions (e.g. asking which European country the user prefers when he/she stated a preference for travelling outside of Europe in a previous question) and will try to always go for the most efficient question to make the interaction as fast as possible.
For every question, the user can answer in one of five possible ways: “It is a must!”, “Would be fine”, “I don’t care”, “I’d rather not”, “Absolutely not!”.
The conversation goes on until the program is sure enough about the user interests. The top 5 university matches are then displayed along with some basic information such as the country, website URL, etc.
University’s perspective
The home university would need to keep a dataset about foreign universities for their students to use. The particular data it chooses to include will depend on its availability; as a general rule, the more the better, let the bot decide if it is useful or not.
Such datasets of information are already available in most universities (for instance, in our case, both UPC’s Telecommunications School and Faculty of Informatics have one, with more detailed information available only to students) as an attempt to present their students with a list of possible destinations.
We provide two sample datasets to show the structure and allow for demoing the program:
- A small one (20 universities) that has been manually curated and allows to show the quality of the obtained results.
- A large one (1000 universities) that has been populated with random data, which means that the results will also be random. It serves to test the program’s efficiency in handling large amounts of data, closer to reality.
Behind the scenes
The program mantains a discrete probability distribution \(P_{user}\) with a value for each university; a high value indicates a good match, and vice versa, and initially is uniform. The university data is represented as a matrix \(M\) of size \(universities \times attributes \); each attribute can use a different scale, such as binary, \([0,1]\) or the real scale.
Then every round the best (unused) question is selected; the criterion that we follow is that of maximizing the separability, taking into account the current user interests up to that point. Being \(a_{q}\) the vector of universities for unused question \(q\) (i.e. a column of \(M\)):
$$Chosen\ question = argmax((P_{user})^T \cdot (a_{avg} - a_{q})^2)$$
where \(a_{avg} = (P_{user})^T \cdot A_{q}\). Essentially, we choose the question with the highest variance, weighting both the variance and the mean by the user distribution.
The user answer is parsed to an integer between 0 and 5, for “Absolutely not!” and “It is a must!” respectively. We then use Bayes’ rule to update the user probabilities given the new answer.
$$P(university | answer) = \frac{P(answer | university) \cdot P(university)}{P(answer)}$$
In our case, being \(ans\) the numerical value for the user answer, \(uni\) vector of attributes for each university to a given question (i.e. a column of \(M\)) and \(prior\) the prior distribution of the user (\(P_{user}\)), we compute the posterior (updated) distribution as:
$$posterior = (1 - abs(ans-uni)) \odot prior$$
We don’t know \(P(answer)\), but it is constant for all universities, so we simply need to normalize the vector in order to make it a probability distribution.
$$posterior \leftarrow \frac{posterior}{\sum_{i=1}^n{posterior_{i}}}$$
Finally, in order to avoid some universities reaching a probability of 0, which happen due to the dataset values and would make them be 0 forever, we apply some smoothing to the distribution using \(\lambda = 0.01\):
$$P_{user} \leftarrow \lambda\mathbf{1} + (1-\lambda)posterior $$
This is repeated until some ending condition is satisfied, usually when some value of \(P_{user}\) is sufficiently high, indicating that a match has been found.
How do I use it?
The code is available at the official repo. Take a look at Telegram’s bot page for instructions on how to set up a bot instance.