Experiments with different hand-coded Support Vector Machine classifiers applied to a variety of datasets.
The problem
Primal version
We defined the SVM as an optimization problem coded in AMPL to be solved by CPLEX. In its primal version, the function to minimize is:
$$ \min_{w, \gamma, s} \quad \frac{1}{2} ||w||^2_2 + \nu \sum_{i = 1}^m s_i $$
subject to:
$$ y_i \left(\sum_{j = 1}^n w_j x_{ij} + \gamma\right) + s_i \geq 1 \quad ; \quad i=1,…,m $$
$$ s_i \geq 0 \quad ;\quad i=1,…,m $$
Where \(w\) are the trainable parameters, \(s_i\) the error for observation \(i\), and \(\gamma\) is a regularization hyperparameter controlling the tradeoff between a good fit to the data and a simple model.
Dual version
In order to deal with non-linear data, we coded the dual version of the previous optimization problem, which allows to use custom kernels. The optimization problem is then:
$$ \max_{\lambda} \quad \sum_{i = 1}^m \lambda_i - \frac{1}{2} \sum_{i = 1}^m \sum_{j = 1}^m \lambda_i y_i \lambda_j y_j K_{ij} $$
subject to:
$$ \sum_{i = 1}^m \lambda_i y_i = 0 $$
$$ 0 \leq \lambda_i \leq \nu \quad ; \quad i=1,…,m $$
Where \(K_{ij} = \phi(x_i)^\top \phi(x_j)\) is a kernel of our choice. In our case, the only kernel used other than the identity one is the Gaussian, defined as:
$$K_{ij} = exp\left(\frac{||x_i-x_j||^2}{2\sigma^2}\right) = \phi(x_i)^\top \phi(x_j)$$
The data
We tested the previous SVMs with the following data:
- A synthetic dataset of linearly-separable data.
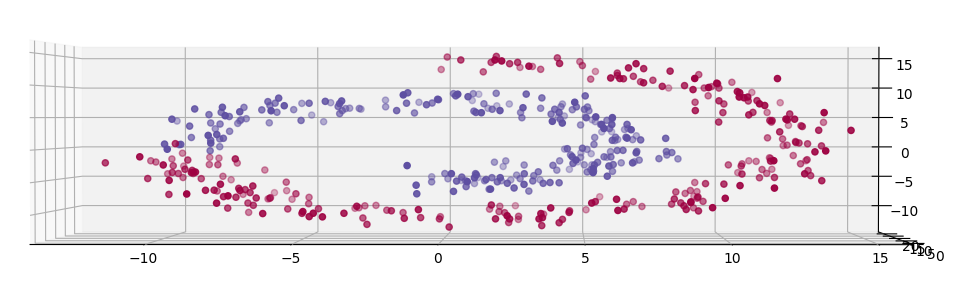
- A synthetic dataset of non-linearly-separable data in a swiss-roll shape, shown in the picture.
- A dataset with real medical data for breast cancer detection.
Results
As expected, when not using the Gaussian kernel, the primal and dual versions give the same solutions, which work well for the linearly-separable data, but are insufficient for more complex cases.
For the real breast cancer dataset, the dual solution obtained an error of ~4%.